Chapter 4 Review

Alright guys, I have been assigned to review extra exciting chapter 4. Here goes...

Okay so 4.1 was all about polynomial functions of a degree greater than 2.
We are aware that...


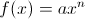
If n=1, the graph of f will be a line through the origin.  If n=2, the graph is a parabola with the vertex at the origin.  If n=3 the graph of the polynomial flattens out around the origin
                          before passing through.

-If n is an odd positive integer, then f is an odd function and the graph of f is symmetric with respect to the origin.
-If n is an even positive integer, the f is an even function and the graph of f is symmetric with respect to the y-axis.   

-As the exponent (n) increases, the graph becomes flatter at the origin. 
The graph will also rise more rapidly for x >1.

-Turning points for a graph of a polynomial are the high and low points of the graphed polynomial. An n-degree polynomial has at most n - 1 turning points. 

In 4.2, we learned the properties of division.

One form of division is titled long division.  This name is by no means an exaggeration. 

Divide x²+3x+1 by x⁴-16

X⁴-16 is not divisible by x²+3x+1, but by long division we can find a quotient and a remainder.

Here it is….            

                                    x²- 3x +8                           Quotient

x²+3x+1   x⁴+0x³+0x²+0x+16                               

                  x⁴+3x³+x²                                                         

                       -3x³-x^{2                                                           subtract}

                        -3x³-9x²-3x                                   

                                   8x²+3x-16                           subtract

                                  8x²+24x+8

                                        -21x-24                          Remainder

Remainder Theorem: If a polynomial f(x) is divided by x - c, then the remainder is f(c).

Factor Theorem: A polynomial f(x) has a factor x - c if and only if f(c) = 0.

In section 4.3, we learned about the zeros of polynomials.

Fundamental theorem of Algebra: if a polynomial f(x) has positive degree and complex coefficients, then f(x) has at least one complex zero.

Theorem on the Maximum Number of Zeros of a polynomial: A polynomial of degree n > 0 has at most n different complex zeros.

Zeros of multiplicity: If a factor x - c occurs m times in the factorization of the polynomial, the c is a zero of multiplicity m of the equation f(x) = 0. 

                - the zero of multiplicity is how many times x - c occurs in the factorization

•     If m is an even number, both ends of the graph of the polynomial point in the same direction
•     If m is an odd number, the two ends of the graph point in opposite directions 

Number of zeros of polynomials: if f(x) has degree n > 0 and if a zero of multiplicity m is counted m times, then f(x) has exactly n zeros.

Descartes' Rule of Signs: there are two parts to this one....

1. The number of positive real zeros of f(x) either is equal to the number of variations of sign in f(x) or is less than that number by an even integer.

2. The number of negative real zeros of f(x) either is equal to the number of variations of sighn in f (-x) or is less than that number by an even integer.

so, for example, if f(x) has three changes in sign, the polynomial either has three positive zeros or one positive zero. Furthermore, if f (-x) only has one change in sign, there is only one negative zero of the polynomial. 

Section 4.4 is about complex and rational zeros of polynomials.

Rule on Conjugate Pair Zeros of a Polynomial: if f(x) has a degree greater than 1 with real coefficients, then...

if z = a+bi (b not equal to zero) is a complex zero, then z = -bi is also a zero of f(x).

Express x⁵-4x³+x²-4 in linear and quadratic polynomials with real coefficients that are irreducible over Ɍ:

= (x⁵-4x³) + (x²-4)                             group terms

= X³(x²-4) + 1(x²-4)                          factor out x³

= (X³+1) + (x²-4)                               factor out x²-4

= (x+1) (x²-x+1) (x+2) (x-2)            factor as the sum of cubes and the difference of squares

and boom! there you have it.

Now, on to finding the possible rational solutions of an equation....

First, one must know that the possible rational zeros are:

    

   Factors of the constant term of the polynomial

Factors of the leading coefficient of the polynomial

     So when given a polynomial, to find the rational solutions of the equation, you find all the choices, positive and negative, for c/d (the numerator divided by the denominator). 

     By dividing synthetically with one of the zeros you obtained, you should see if when divided, the remainder if zero.  If it is, that factor is a rational solution of the equation. 

    Keep dividing by the choices of c/d until you have gone through all of them. Remember, if a factor does come to zero, use the new polynomial formed when continuing synthetic dividing. 

    

Finally, on to 4.5. This section is all about rational functions.

A function is rational if:

 

, where g(x) and h(x) are polynomials.  The domain of f consists of all real numbers except the zeros of the denominator h(x).

Definition of a vertical asymptote: The line x = a is a vertical asymptote for the graph of a function if

                                           as x approaches a from either the left or the right.

Definition of a horizontal asymptote: The line y = c is a horizontal asymptote for the graph of f if:

f(x) approaches c as x approaches infinity or negative infinity.

Guidelines for Sketching the Graph of a Rational Function

1. Find the x-intercepts (the real zeros of the numerator g(x) ) and plot the points on the x-axis

2. Find the real zeros of the denominator h(x).  For each real zero a, sketch the vertical asymptote x = a with dashes.

3. Find the y-intercept f (0), if it exists, and plot the point (0, f (0) ) on the y-axis.

4. If there is a horizontal asymptote x = c, sketch it with dashes.

5. Sketch the graph of f in each of the regions on the xy plane determined by the vertical asymptotes.

And there you have it folks; chapter 4 in a nutshell. Hope it helps

Chapter 2 Review

Chapter 2 Review

So here's a basic summary of what we learned in Chapter 2- Equations and Inequalities

-An Equation is a statement that 2 quatities or expressions are equal

-A linear equation is an equation that is written in the form ax+b=0 where a does not equal 0.

Solving a Linear equation








-Simple Interest Formula
I=Prt where I is the simple interest, P is the principal amount, r is the interest rate, and t is time.


-Zero Factor Theorem



-Special Quadratic Equation



-Completing the Square- There are 2 ways to complete the square, depending on on the sign of the equation.

If the sign is positive, the equation is:


If the sign is negative, the equation is:


-Quadratic Formula- The quadratic formula is used when an equation is unable to be factored easily, so you use this formula to get the value(s) of x.



-Properties of i



Conjugate of a Complex number: If.... (z=a+bi) then its conjugate is...a-bi

ex. Complex #- 8+4i
Conjugate- 8-4i

-Solving an equation using grouping




-Inequalities: an inequality is a statement that 2 quatities or expressions are not equal.

Solving an inequality



-Properties of Absolute Values




ex.






-Solving a Quadratic Inequality


Then, use the values of x on a number line and plug in numbers (I used -5, 0, and 5) in the different intervals to find if that interval is positive or negative.

So the answer would be:


Well that's about all we did in Chapter 2. Good luck on the final.

-Michael Levitsky

5.4

Hello everyone!

So as far as five four goes, it’s just building off of five three’s ideas. To start it all off, let’s review:

Last section told us that log has a subscript 10 (common log) and that ln has a subscript e (natural log). Now that we have that covered, moving onto the…

Law of Logarithms.

1) log_a(uw) = log_au + log_aw

2)log_a(u/w) = log_au - log_aw

3)log_a(u^c) = c log_au

Easy enough, right? Now to le comparisons.

Common Logarithms	Natural Logarithms
log(uw) = logu + logw	ln(uw) = lnu + lnw
log(u/w) = logu – logw	ln(u/w) = lnu – lnw
log(uc) = c logu	Ln(uc) = c lnu

There are no differences in the way you play out these logarithms, just differences in the meanings.

BUT, BEWARE. THERE IS A SLIGHT CATCH. Log_a(u+w) does NOT translate to log_au + log_aw. Also, log_a(u-w) does NOT translate to log_au – log_aw. This isn’t like f(x) in those ways at all!

     ^ You can’t have a log of a negative number, that’s why -4 doesn’t work.

Onward again, 

So I think that’s about it, I hope this helped!

Have a great weekend!

P.s. COME TO FALL PLAY TOMORROW AT 2 PM. MR WILHELM WENT TONIGHT(sorry I didn't say hi to you) SO YOU SHOULD GO TOMORROW.

Kristy :]

Section 5.1 and 5.2 (Glavin)

Exponential functions are defined as this (f with base a): F(x)=a^x for every x in the domain, where a>0 and a≠1.
The graph for a>1 looks like this:

The graph for when 0 < a < 1 looks like this:

Note: The top graph is displaying exponential growth, and the bottom graph exponential decay.

Exponential functions are also one to one. The exponential F(x)=a^x for a<0<1 or a>1 is one to one. The following conditions are satisfied for the real number j and k.
1) If j ≠ k, then a^j ≠ a^k
2) If A^j = A^k, then j = k


Solving an exponential equation is also really easy.
For example:
3^(5x-8)=9^(x+2)
first step, you want to get both sides to have to same base. In this situation, you take the square root of 9.
3^(5x-8)=3^2(x+2)
Now, you just multiply the 2 through the x+2
3^(5x-8)=3^(2x+4)
since exponential functions are one to one, you now say that the exponents are equal.
5x-8=2x+4
solve from there.
3x=12
x=4

Exponential functions can also be stretched and shifted.

In example, this graph:


Shows an exponential graph that has been stretched vertically!

When you shift the graph, the graph either moves up for down or left and right. For the graph to move up or down, you change the constant. in example: 3^(x)-2 shifts the graph down 2 units. To move it right and left, you add or subtract from the exponent. In example: Y=3^(x) is shifted to the right when you subtract 2 from the exponent, creating the formula Y=3^(x-2).


Also learned in section 5.1 is the compound interest formula, which will be used greatly in the next section.


Section 5.2

Using the equation literally right above us, we will solve this problem:

Suppose 1000 monetary units is invested at a compound interest rate of 9%. Find the new amount of principal after one year if the interest is compounded yearly.

If we fill in the equation given above, we get A=1000(1+[.09/1])^1
R is .09, which is the rate of interest.
N is the amount of times per year which we interested, which was 1.
T is usually one, unless you are doing it over a span of multiple years. In this situation, it is one.
P is the amount of starting principal we had, which in this case would be 1000 dollars.
A is the accumulated amount of wealth.

If we simplify the equation, we learn the amount of money earned is 1090 monetary units. If we do this and skip step 3 repeatedly, we earn infinitie monies.
Step 1: deposit money
Step 2: Earn money every year
Step 3: ????
Step 4: Infinitie monies!!!
#Forever Alone

We also learned this section what natural exponential function was.
The equation given for that is: f(x)= e^x
for every real number x.

The equation for the continuously compounded interest formula is as follows:

A=Pe^(rt),
where P = principal
r = annual interest rate expressed as a decimal
t = number of years P is invested
A = Amount of t years

Another thing you will need to know in this section is the law of growth/decay formula. This is used when q is changed instantaneously at a rate that is proportional to the current value:
q = q(t) = (q(subscript 0)e)^n
where r>0 is the rate of growth, and r<0 is the rate of decay.

Thats all we learned in these two sections really.
Guess I'm done.
-Glav-Glav