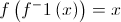4.1 Polynomial Functions of Degree Greater Than 2

A polynomial function can be written in this form:

-a is a coefficient

-n is a whole number (non negative integer)

Any polynomial function has domain with all real numbers. This is because a polynomial function doesn't have any denominators or radicals that contain variables.

A polynomial function always has a y-intercept but not necessarily an x-intercept(s).

Linear Function (degree of 1)

Quadratic Function (degree of 2)

Cubic Function (degree of 3)

-The degree of a function is equal to the maximum number of x-intercepts the function can have.

Intermediate Value Theorem- If f is a polynomial function and f(a) doesn't equal f(b) for a < b, then f takes on every value between f(a) and f(b) in the interval [a,b]

The bottom or top of a curve in a polynomial function's graph is the relative minimum or maximum. A value f(a) is a relative maximum of f if on the interval (x1,x2) (that includes a), f(a)>f(b) for any x2>b>x1.

-These points are called extrema

-The maximum number of extrema a polynomial function can have is equal to one less than the degree. (n-1)

End Behavior

As the you go to the left, the x values approach - ∞

As you go to the right, the x values approach ∞

From left to right, the behavior of the y (f(x)) values is dependent on the degree of the function.

-an even degree means that the right and left ends will be going in the same direction

-an odd degree means that the right and left ends will be going in opposite directions.

The leading coefficient tells what direction the right end goes (negative coefficient: negative infinity, positive coefficient: infinity)

ex.

left: x --> -∞ f(x) --> -∞

right: x--> ∞ f(x) --> ∞

Zeros of Multiplicity

if

find zeroes and its

The zero of multiplicity is 2, equal to to the power of the factor. A function with zeroes of multiplicity equaling 2, the extrema of the curve is tangent to the x-axis.

If the zero of multiplicity is 3, the graph levels out before passing through the x-axis and then continues.

Function #1 has a degree of 3, because it passes through the x-axis 3 times and none of those times is the graph tangent to the x-axis or does the graph level out then continue.

Function #2 has a degree of 4, because it is tangent (zero of multiplicity 2) to the graph once and then passes through 2 more times. 2+1+1=4

Function #3 has a degree of 6, because it is tangent once, passes through once, and levels out and continues once. 2+1+3=6

Thats it!

3.9 Variation

Hello everyone! Today, after eating cake and brownies for Mr. W's birthday, we learned about variation.


Variation is used to describe relationships between variable quantities.

The graph of y=kx is linear,

And the graph of y=k/x looks like this:

The book gives guidelines to solving variation problems:

1. Write a general formula using the variables and k (the constant of variation).
2. Find the value of k using the given values.
3. Put the value of k that you found in guideline 2 into the equation, giving you the specific equation for that problem.
4. Use your new formula (involving the value of k) to solve the problem.

An example problem (Example 3 on page 248):

A variable w varies directly as the product of u and v and inversely as the square of s. 

       

        a. If w = 20, when u = 3, v = 5, and s = 2, find the constant of variation (k). 

        b. Find the value of w when u = 7, v = 4, and s = 3.

The general formula for w is:

Now, we can do part a, plugging in the numbers given for the variables:

For part b, all we need to do is plug the values given for the variables and the value of k into the general formula:

Extra tips: When the problem says that one thing (ex. weight) varies directly/proportionally with something else (ex. product of length and width), it means that you are multiplying by the constant. If it varies inversely, you divide the constant by it.

That's all, I guess. Have a good rest of you evening everyone and

HAPPY BIRTHDAY MR. WILHELM!!!

- Jessica Harrison

3.8 Inverse Functions

Mr. Wilhelm taught us about inverse functions ever so perfectly, but the wheel has chosen me to sum it up.

Two function, f and g, are inverses of each other if and only if
                               

One-to-One
A function is one-to-one if it passes the horizontal line test (every horizontal line intersects the graph in at most one point) and if

 -----> 

3a+2=3b+2

3a=3b

a=b

A function that is increasing throughout its domain is one-to-one.

A function that is decreasing throughout its domain is one-to-one.

Finding

1) Verify that f is a one-to-one function

2) Solve the equation y=f(x) for x in terms of y, obtaining an equation of the form                     

x=(y)

3) Verify that:

 for every x in the domain of f

 for every x in the domain of 

There are many examples in the book if you need them.

Remember, always keep the Wilhelm philosophy in mind, "Learn and the grades will follow," and "Eleni is always right."

HAPPY BIRTHDAY THAD!

Joseph "The Preston" Nagridge

Happy Birthday Mr. Wilhelm!

Happy Birthday Mr. Wilhelm!!!!!!

3.7 Operations on Functions 10/18/11

In this section, we looked at defining functions using various operations and combining multiple expressions using new methods.

First, we will take a look at the basic operations of functions: sum, difference, product, and quotient.

Sum:

---->  


Difference:

  ---->  


Caution: Remember to distribute the negative when inserting the g(x) expression.

Product:


  ---->


Quotient:


    ---->  



A sample of the sum method:




Find
Since this^^ = 
Then:






Next, we began to look into compositie functions.

The composite function  f  ° g  of two functions f  and g is defined by:

(f  ° g)(x) = f(g(x))


The domain of  f  ° g is the set of all x in the domain g such that g(x) is in the domain of f.

An example of a composite function problem:

Let  and 

(f  ° g)(x) 

(f  ° g)(x)

(f  ° g)(x)

(f  ° g)(x)

Domain problems are also common in this section, so be ready to find the domain of functions like we did in previous chapters.

Hope this helped!

-julia