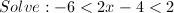2.7 - More on Inequalities

This chapter deals with mostly polynomial inequalities and it builds off of many of the topics discussed last chapter













Necessary Information:














To solve an inequality involving polynomials of degree greater than 1, we shall express each polynomial as a factor (i.e. ax + b and/or ax²+bx+c). If a factor is not zero in an interval then it is either positive or negative throughout the interval. So if we chose any point in the interval, and the factor is positive or negative for x=k , then it is positive or negative throughout the interval. The value of the factor at x=k is called the test value of the factor at test number k. This is shown in the following example













Ex #1 Solving a quadratic inequality













Solve the inequality 2x² - x < 3.


Solution: To use test values you have to have a 0 on one side of the equality sign (exactly like when solving a quadratic equation) do the following

2x² - x < 3 Given

2x² - x - 3 < 0 Make one side 0

(x + 1)(2x - 3) < 0 Factor

The factors x + 1 and 2x - 3 are zero -1 and 3/2, respectively. So the the nonintersecting intervals are

(-inf., -1), (-1, 3/2), and (3/2, inf.)

A way to find the sign of x + 1 and 2x - 3 we can make a sign chart by applying the laws of signs to the product factors the resulting sign is positive or negative according to whether the number of negative signs of factors is even or odd, respectively

Interval "(-inf., -1)" "(-1, 3/2)" "(3/2, inf.)"

sign x + 1 negative positive positive

Sign 2x - 3 negative negative positive

Result positive negative positive


This is a very basic idea on how to solve a quadratic inequality

Alex Florias

Chapter 2.6 - Inequalities

Important Terms to Know:

• Inequality - A statement that two quantities or expressions are NOT equal
• Open Interval - an open interval is used to illustrate the solution of an inequality that consists of every real number between the two given restrictions, but NOT the given numbers surrounding x. Parentheses, "(" and ")", are used to denote an open interval.
• ex: 4<x<8 - (4, 8) 

• Closed Interval - a closed interval is used to illustrate the solution of an inequality that consists of every real number between the given restrictions, INCLUDING the given numbers surrounding x. Brackets, "[" and "]", are used to denote a closed interval. 

• ex: 3<x<7 - [3, 7] 

• Half-Open Interval - a half-open interval is used to illustrate the solution of an inequality containing both a less-then/greater-than and a less-than or equal-to/ greater-than or equal-to. 
• ex: 6>x>-3 - (6, -3] 

• Infinite Interval - an infinite interval is used to illustrate the infinite solutions of an inequality higher or lower than than the given restriction. parentheses are used next to the ∞ symbol. 
• ex: 5<∞ - (5, ∞] 

Properties of Inequalities

*It's important to remember that when multiplying or dividing both sides of an inequality by a negative real number REVERSES the inequality sign.

Solving an Inequality

ex #1

                 subtract 5 from both sides

                                   divide both sides by -6         

*  remember to reverse the inequality sign         

       x consists of all real numbers such that x>-2

                                                 write as interval 

ex #2

A real number x is a solution of the given inequality if and only if it is a solution of BOTH inequalities

Solve the first inequality: 

                              add 4 to both sides

                                                            simplify

                                      divide both sides by 2

                                                               simplify

                                          equivalent inequality

Now solve the second equation:

                                          add 4 to both sides

                                      divide both sides by 2

x is only a solution of the given inequality if and only if BOTH x>-1 AND x<3, or it could be written as -1<x<3

You could also solve the equation using this shorter, alternative method:

                                                    add 4 

                                                         simplify 

                                                     divide by 2

Solving a Rational Inequality

since the numerator is positive, the fraction is positive if and only if the denominator, x-2, is also positive. Thus, x-2>0 or, equivalently, x>2, and the solutions are all real numbers in the infinite interval (2, ∞). 

The Lens Formula 

If a convex lens has a focal length of f units and if an object is placed a distance p units from the lens with p>f, then the distance q from the lens to the image is related to p and f by the formula:

Union Symbol 

the union symbol unites two collections of points

Intersection Symbol

Properties of Absolute Values (b>0)

Good Luck everyone!! Rock on!!

By Austin Kellogg

Chapter 2.4 - Complex Numbers

This chapter in the book has to do with complex numbers. A complex number is a number that has both real and imaginary terms. An imaginary number is any number that results in a negative number whenever it is squared. Imaginary numbers are used to give an answer to problems that normally would (and still technically do) have no solution.

The imaginary number is written 'i' and is equal to . It is treated as a variable until it can be squared at which point it can obviously be reverted to -1

They are helpful for solving negative square roots and solving the quadratic formula.

EXAMPLE #6

convert to quadratic formula

multiply and subtract

substitute i for

simplify

making the solutions

and

It's really not too hard to deal with once you get the hang of it, so good luck.

Dan O'Neil