- Inequality - A statement that two quantities or expressions are NOT equal
- Open Interval - an open interval is used to illustrate the solution of an inequality that consists of every real number between the two given restrictions, but NOT the given numbers surrounding x. Parentheses, "(" and ")", are used to denote an open interval.
- ex: 4<x<8 - (4, 8)
- Closed Interval - a closed interval is used to illustrate the solution of an inequality that consists of every real number between the given restrictions, INCLUDING the given numbers surrounding x. Brackets, "[" and "]", are used to denote a closed interval.
- ex: 3<x<7 - [3, 7]
- Half-Open Interval - a half-open interval is used to illustrate the solution of an inequality containing both a less-then/greater-than and a less-than or equal-to/ greater-than or equal-to.
- ex: 6>x>-3 - (6, -3]
- Infinite Interval - an infinite interval is used to illustrate the infinite solutions of an inequality higher or lower than than the given restriction. parentheses are used next to the ∞ symbol.
- ex: 5<∞ - (5, ∞]
Properties of Inequalities
*It's important to remember that when multiplying or dividing both sides of an inequality by a negative real number REVERSES the inequality sign.
Solving an Inequality
ex #1
* remember to reverse the inequality sign
ex #2
A real number x is a solution of the given inequality if and only if it is a solution of BOTH inequalities
Solve the first inequality:
Now solve the second equation:
x is only a solution of the given inequality if and only if BOTH x>-1 AND x<3, or it could be written as -1<x<3
You could also solve the equation using this shorter, alternative method:
Solving a Rational Inequality
since the numerator is positive, the fraction is positive if and only if the denominator, x-2, is also positive. Thus, x-2>0 or, equivalently, x>2, and the solutions are all real numbers in the infinite interval (2, ∞).
The Lens Formula
If a convex lens has a focal length of f units and if an object is placed a distance p units from the lens with p>f, then the distance q from the lens to the image is related to p and f by the formula:
Union Symbol
the union symbol unites two collections of points
Intersection Symbol
Properties of Absolute Values (b>0)
Good Luck everyone!! Rock on!!
By Austin Kellogg













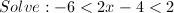


























No comments:
Post a Comment