Okay so 4.1 was all about polynomial functions of a degree greater than 2.
We are aware that...
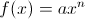
If n=1, the graph of f will be a line through the origin. If n=2, the graph is a parabola with the vertex at the origin. If n=3 the graph of the polynomial flattens out around the origin
before passing through.
-If n is an odd positive integer, then f is an odd function and the graph of f is symmetric with respect to the origin.
-If n is an even positive integer, the f is an even function and the graph of f is symmetric with respect to the y-axis.
-As the exponent (n) increases, the graph becomes flatter at the origin.
The graph will also rise more rapidly for x >1.
-Turning points for a graph of a polynomial are the high and low points of the graphed polynomial. An n-degree polynomial has at most n - 1 turning points.
In 4.2, we learned the properties of division.
One form of division is titled long division. This name is by no means an exaggeration.
Divide x2+3x+1 by x4-16
X4-16 is not divisible by x2+3x+1, but by long division we can find a quotient and a remainder.
x2+3x+1 x4+0x3+0x2+0x+16
-3x3-x2 subtract
8x2+3x-16 subtract
-21x-24 Remainder
Remainder Theorem: If a polynomial f(x) is divided by x - c, then the remainder is f(c).
Factor Theorem: A polynomial f(x) has a factor x - c if and only if f(c) = 0.
In section 4.3, we learned about the zeros of polynomials.
Fundamental theorem of Algebra: if a polynomial f(x) has positive degree and complex coefficients, then f(x) has at least one complex zero.
Theorem on the Maximum Number of Zeros of a polynomial: A polynomial of degree n > 0 has at most n different complex zeros.
Zeros of multiplicity: If a factor x - c occurs m times in the factorization of the polynomial, the c is a zero of multiplicity m of the equation f(x) = 0.
- the zero of multiplicity is how many times x - c occurs in the factorization
- If m is an even number, both ends of the graph of the polynomial point in the same direction
- If m is an odd number, the two ends of the graph point in opposite directions
Number of zeros of polynomials: if f(x) has degree n > 0 and if a zero of multiplicity m is counted m times, then f(x) has exactly n zeros.
Descartes' Rule of Signs: there are two parts to this one....
1. The number of positive real zeros of f(x) either is equal to the number of variations of sign in f(x) or is less than that number by an even integer.
2. The number of negative real zeros of f(x) either is equal to the number of variations of sighn in f (-x) or is less than that number by an even integer.
so, for example, if f(x) has three changes in sign, the polynomial either has three positive zeros or one positive zero. Furthermore, if f (-x) only has one change in sign, there is only one negative zero of the polynomial.
Section 4.4 is about complex and rational zeros of polynomials.
Rule on Conjugate Pair Zeros of a Polynomial: if f(x) has a degree greater than 1 with real coefficients, then...
if z = a+bi (b not equal to zero) is a complex zero, then z = -bi is also a zero of f(x).
Express x5-4x3+x2-4 in linear and quadratic polynomials with real coefficients that are irreducible over Ɍ:
= (x5-4x3) + (x2-4) group terms
= X3(x2-4) + 1(x2-4) factor out x3
= (X3+1) + (x2-4) factor out x2-4
= (x+1) (x2-x+1) (x+2) (x-2) factor as the sum of cubes and the difference of squares
and boom! there you have it.
Now, on to finding the possible rational solutions of an equation....
First, one must know that the possible rational zeros are:
Factors of the constant term of the polynomial
Factors of the leading coefficient of the polynomial
So when given a polynomial, to find the rational solutions of the equation, you find all the choices, positive and negative, for c/d (the numerator divided by the denominator).
By dividing synthetically with one of the zeros you obtained, you should see if when divided, the remainder if zero. If it is, that factor is a rational solution of the equation.
Keep dividing by the choices of c/d until you have gone through all of them. Remember, if a factor does come to zero, use the new polynomial formed when continuing synthetic dividing.
Finally, on to 4.5. This section is all about rational functions.
A function is rational if:
, where g(x) and h(x) are polynomials. The domain of f consists of all real numbers except the zeros of the denominator h(x).
Definition of a vertical asymptote: The line x = a is a vertical asymptote for the graph of a function if
as x approaches a from either the left or the right.
Definition of a horizontal asymptote: The line y = c is a horizontal asymptote for the graph of f if:
f(x) approaches c as x approaches infinity or negative infinity.
Guidelines for Sketching the Graph of a Rational Function
1. Find the x-intercepts (the real zeros of the numerator g(x) ) and plot the points on the x-axis
2. Find the real zeros of the denominator h(x). For each real zero a, sketch the vertical asymptote x = a with dashes.
3. Find the y-intercept f (0), if it exists, and plot the point (0, f (0) ) on the y-axis.
4. If there is a horizontal asymptote x = c, sketch it with dashes.
5. Sketch the graph of f in each of the regions on the xy plane determined by the vertical asymptotes.
And there you have it folks; chapter 4 in a nutshell. Hope it helps



No comments:
Post a Comment