exponentiation is what is being done to X in this case.
To solve, we need to undo what is being done to X, which is a logarithm :)
Mr. Wilhelm's KEY TO EVERYTHING!
That is how to rewrite an exponential function as a logarithmic function. With this, we can solve exponential equations that would otherwise be unsolvable!
This is how you might apply a logarithm to an exponential function. As you can see, Y=1,000 A=10 and X=3
The key to everything is as easy as that :)
Special Logarithms!
When it is just written "log" with no subscript, it is implied that it is log10 -- COMMON LOG!
When it is written ln, it is implied that it is loge -- NATURAL LOG!
How to graph a logarithm!
A few other little tidbits to know:
since the domain of an exponential function is (-∞, ∞), so thats the RANGE of a logarithm
the range of an exponent is (0, ∞), so thats the DOMAIN of a logarithm. (unless it has been moved by the C value)
*Exponents and Logarithms are 1 to 1*
Sorry, there are no pretty logarithm pictures on the internet :(
Links and stuff:
http://www.themathpage.com/aprecalc/logarithms.htm
http://www.sosmath.com/algebra/logs/log1/log1.html
http://www.purplemath.com/modules/logs.htm
http://www.shodor.org/unchem/math/logs/index.html
http://www.youtube.com/watch?v=mQTWzLpCcW0
And, just for old time's sake :
Nonagon Song - http://www.youtube.com/watch?v=x5ohtlewREI
One Dozen Monkeys -http://www.youtube.com/watch?v=2qdql9vsWWM&feature=related
Hope this helped and made logarithms a little less unbearable :)
Bye, Katie

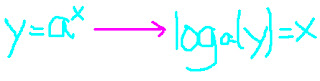







 or one as simple as y=mx+b, but thats not as fun......
or one as simple as y=mx+b, but thats not as fun......